DataStructure_Algorithm_HandBook_PreForLeetCode
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Example 1:
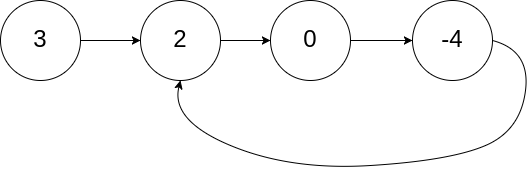
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
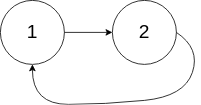
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range
[0, 104]. -105 <= Node.val <= 105posis-1or a valid index in the linked-list.
Follow up: Can you solve it using O(1) (i.e. constant) memory?
Solution:
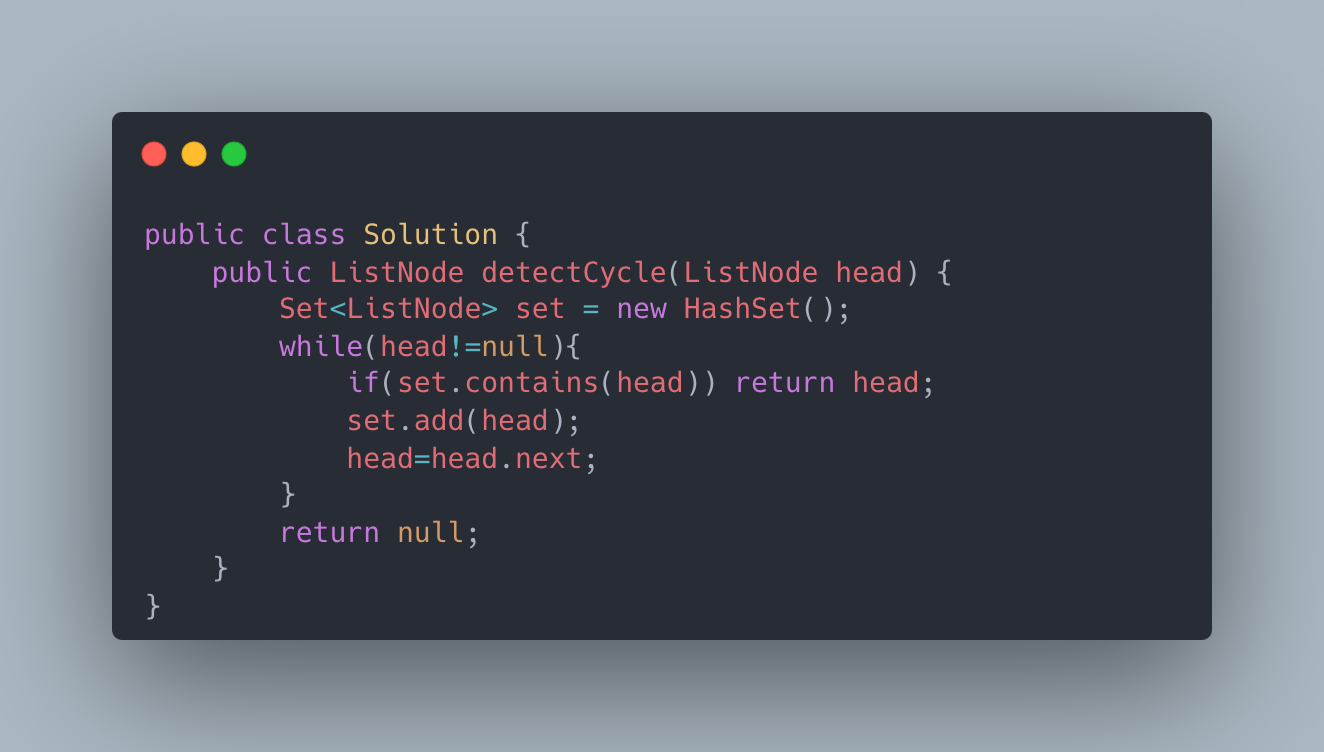
The most intuitive feeling for this problem is to use a hash table. Every time a node is accessed, it is judged whether the node exists in the hash table. If it exists, it indicates a loop and returns the node directly. Otherwise, just put the node into the hash table. If it has not returned until the end of the linked list, null is returned. The time complexity of this method is O(n), but the space is also O(n), which is not the optimal solution.
The best solution to this problem is to use double pointers. We use two pointers, fast and slow.
They all start at the head of the linked list. Subsequently, the slow pointer moves backward one position at a time, while the fast pointer moves backward two positions. If there is a cycle in the linked list, the fast pointer will eventually meet the slow pointer in the cycle again.
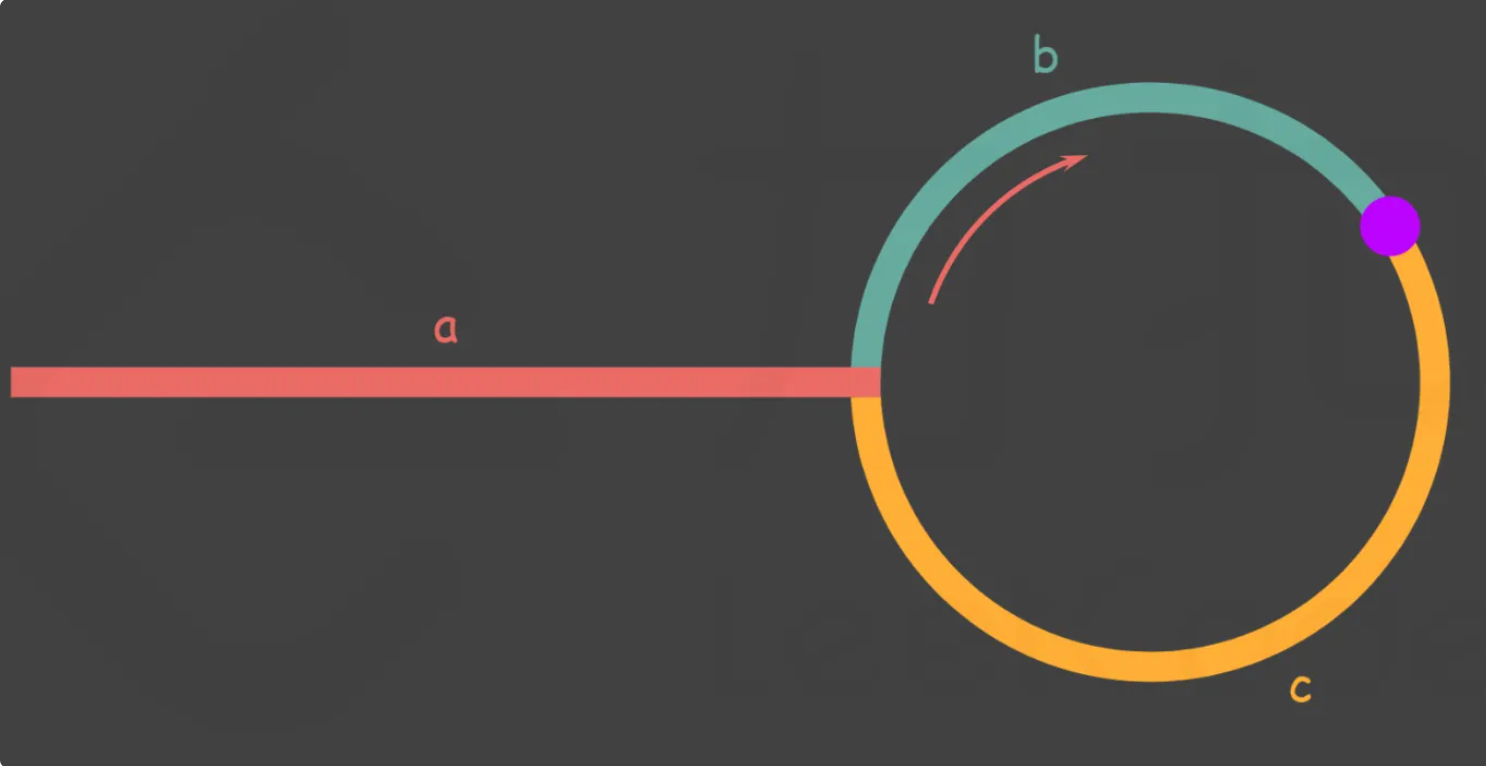
As shown in the figure, let the length of the outer part of the linked list be a. After the slow pointer enters the ring, it travels a distance b to meet fast. At this point, the fast pointer has completed n rounds of the ring, so the total distance it has traveled is a+n(b+c)+b=a+(n+1)b+nc
According to the meaning of the question, at any time, the distance traveled by the fast pointer is twice that of the slow pointer.
Therefore, we have
a+(n+1)b+nc=2(a+b) a=c+(n−1)(b+c)
With the equivalence relationship a=c+(n−1)(b+c).
We will find that: the distance from the meeting point to the loop entry point plus the loop length of n−1 circles is exactly equal to the distance from the head of the linked list to Distance from the loop entry point.
Therefore, when we find that slow and fast meet, we use an additional pointer ptr.
Initially, it points to the head of the linked list;
subsequently, it and fast move backward together one position at a time.
Eventually, they will meet at the loop entry point.